고정 헤더 영역
상세 컨텐츠
본문
📝 벡터(vector)
- 기하학적으로 벡터를 방향을 가진 선분 즉, 화살표로 표현한다.
- 벡터의 속성은 ‘길이(혹은 크기)’와 ‘가리키는 방향’
- ‘위치’는 벡터의 속성이 아니다.
따라서 다른 위치에 있더라도 동일한 길이와 방향을 가리키는 두 개의 벡터는 동일한 것으로 취급된다.
예를 들어, 아래의 그림에서 벡터 u와 v는 동일하다.
- 크기와 방향을 모두 갖는 물리량을 모델링하는 데 유용하다.
ex) 빛이 비추는 방향, 다각형의 방향, 3D 세계에서의 카메라가 보고 있는 방향 등

보통 벡터를 표시할 때는 굵은 소문자를 이용하지만 굵은 대문자를 이용하는 경우도 있다.
다음은 각각 2차원, 3차원, 4차원 벡터의 표시 예이다. 혹은 화살표를 사용하여 표기하기도 한다: a→
u=(ux,uy),N=(Nx,Ny,Nz),c=(cx,cy,cz,cw)
▪️ 벡터의 크기 계산
기하학적으로 벡터의 크기는 방향을 가진 선분의 길이이다.
벡터의 성분이 주어졌다고 할 때, 다음과 같은 식을 이용해 벡터의 크기를 대수학적으로 계산해낼 수 있다.
||u||=ux2+uy2+uz2
ex) u=(1,2,3)과 v=(1,1) 벡터의 크기를 구하라.
||u||=12+22+32=1+4+9=14

마찬가지로, 위의 식을 2차원으로 일반화하면 다음과 같이 v를 얻을 수 있다.
||v||=12+12=2
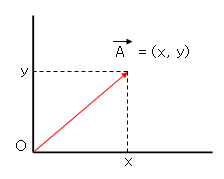
📌 연관 ▶ #피타고라스의 정리
▪️ 영 벡터와 단위 벡터
영 벡터란 모든 성분에 0을 가진 것이다.
영 벡터는 굵은 0으로 표시된다: 0=(0,0,0)
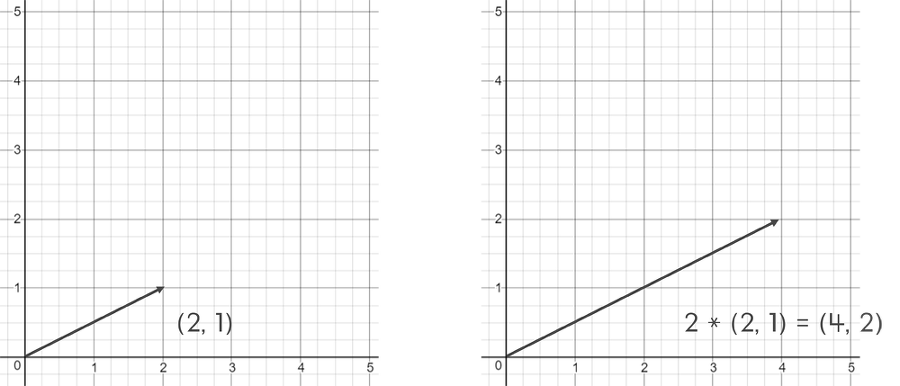
단위 벡터란 크기가 1인 벡터이다.
곱셈에서, 1∗n=n일 때 n에 어떤 수를 넣더라도 항상 n이 나오도록 하는 1을 곱셈에서의 항등수라고 한다.
벡터에서도 값과 벡터가 곱해질 때 단위 벡터는 항등수에 해당한다.
단위 벡터는 크기가 1이고 방향을 가지고 있으므로, 여기에 값을 곱해주면 방향은 같지만 크기가 다른 벡터를 마음대로 만들 수 있다.
혹은 크기는 무시하고 방향만 나타내기 위해서 사용한다.
모든 벡터는 정규화(normalize) 과정을 거쳐 단위 벡터로 만들 수 있다.
단위벡터의 용도는 일반적으로 회전의 중심축으로써 사용되는 경우가 많다.
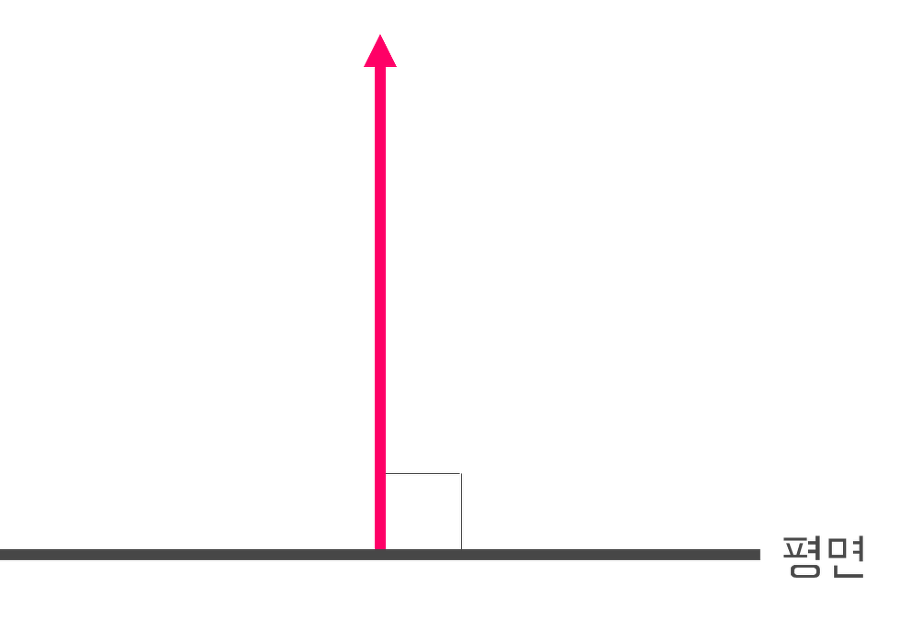
그 외에도 삼각형면의 법선 벡터(normal vector) 역시 단위벡터를 사용한다.
법선 벡터란, 평면에 수직인 벡터이다.
▪️ 벡터의 정규화
벡터의 정규화란 벡터의 크기를 1로 만들어 단위 벡터가 되도록 하는 것이다.
다음과 같이 벡터의 각 성분을 벡터의 크기로 나누면 정규화가 된다.
단위 벡터는 위에 모자를 씌워 표기한다: u^
u^=u||u||=(ux||u||,uy||u||,uz||u||)
ex) u=(1,2,3) 벡터를 정규화하라.
u^=u14=(114,214,314)
📝 스칼라(scalar)
- 크기와 방향을 가지는 벡터에 대비되는 개념
- 단지 크기만 있는 물리량이다.
- 좌표계가 변환되어도 그에 따라 변화하지 않는 양, 단순히 ‘하나의 숫자’이다.
▪️ 벡터와 스칼라의 연산
스칼라는 벡터와의 곱셈 연산을 통해 벡터의 크기를 조정하는 데 사용된다.
스칼라 연산은 벡터의 방향에는 영향을 미치지 않으며 단지 벡터의 크기만을 바꿀 뿐이다.
각 항에 스칼라를 곱해주면 된다. 만약 음수를 이용하는 경우에는 벡터의 방향이 뒤집힌다.
즉, 벡터에서 부호는 방향을 결정하는 역할을 한다.
ku=(kux,kuy,kuz)
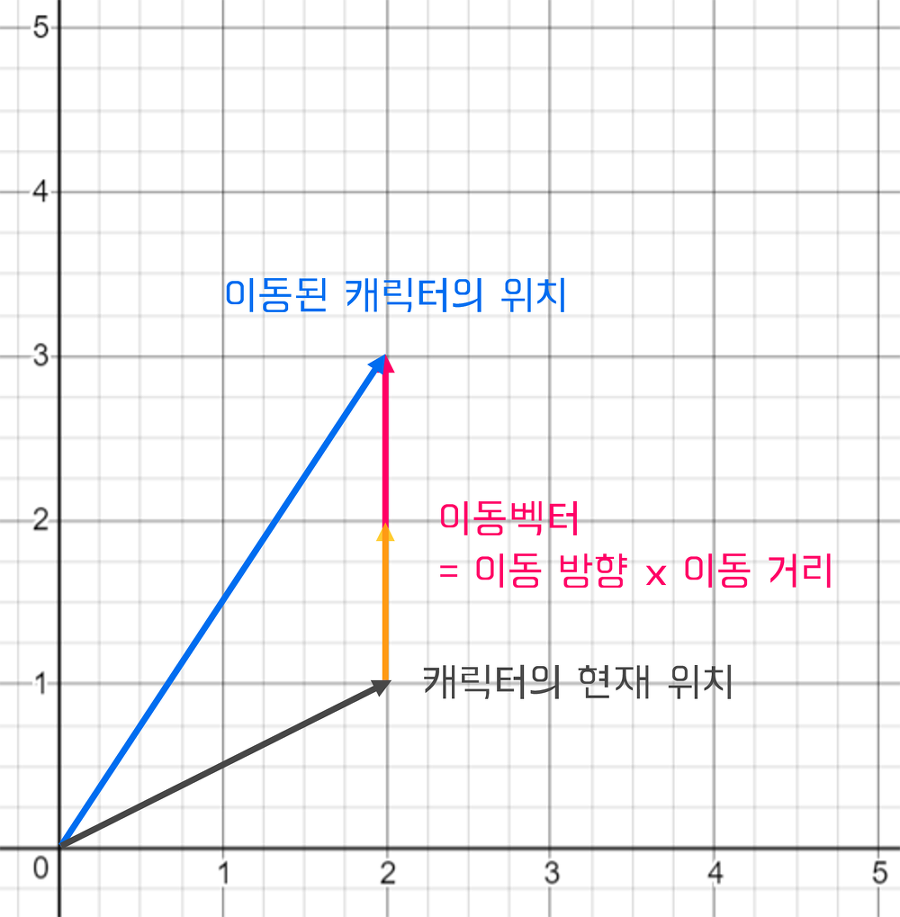
게임에서 캐릭터를 이동시킬 때, 단위벡터와 스칼라의 곱을 사용한다.
캐릭터를 이동시킬 방향(단위벡터)에 이동하고자 하는 거리(스칼라) 값을 곱하면,
캐릭터가 이동할 벡터를 구할 수 있다.
즉, 캐릭터의 위치 벡터에 이동 벡터를 더하여,
최종적으로 캐릭터가 이동될 위치를 구해 캐릭터를 그 위치로 이동시키면 된다.
▪️ 역벡터
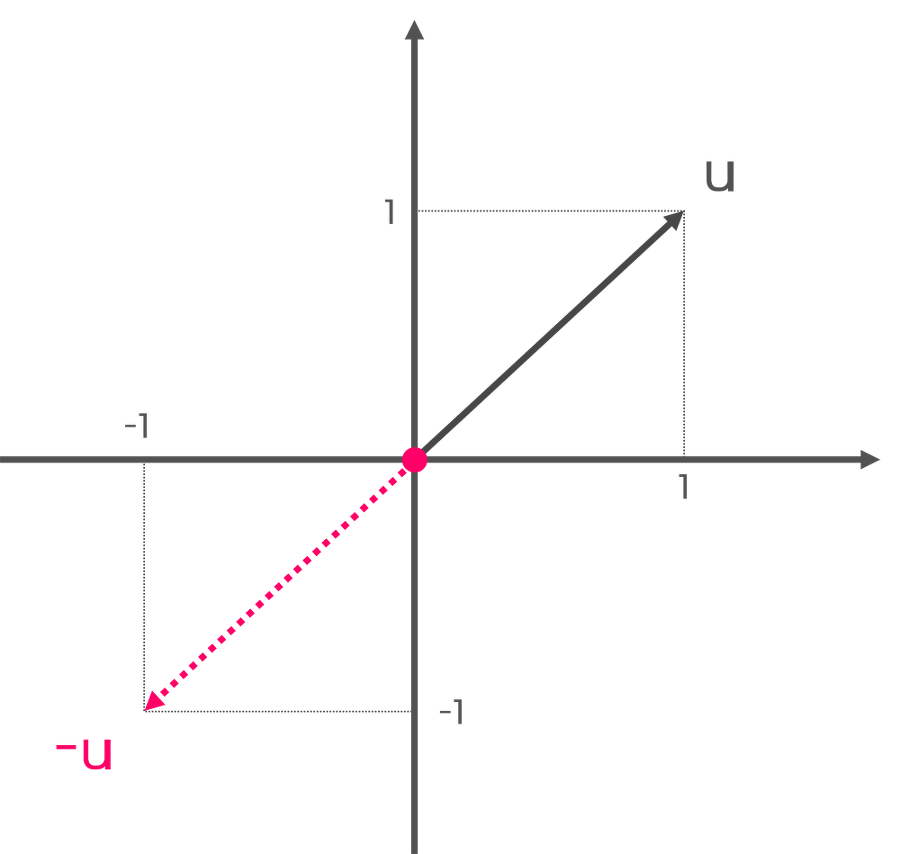
역벡터란 크기는 같으나 방향이 서로 반대인 벡터를 말한다.
역벡터는 벡터 앞에 -(음부호)를 붙여서 표시를 한다.
-(음부호)의 역할은 벡터의 방향을 바꾸는 역할을 하며, 각 성분에 -1을 곱한 것과 같다.
예를 들어 (1, 1) 벡터에 -1을 곱해주면 크기는 그대로지만 방향이 반대가 된다는 것을 아래 그림을 통해 알 수 있다.
'Study > Discrete math' 카테고리의 다른 글
| 벡터 대수 (0) | 2023.02.05 |
|---|---|
| 벡터의 외적(Cross Product)과 내적(Inner Product) (0) | 2022.10.25 |
| 왼손 좌표계(Left-handed coordinate system)와 오른손 좌표계(Right-handed coordinate system) (0) | 2022.06.09 |
| 벡터의 연산 - 덧셈과 뺄셈, 분해 (0) | 2022.06.09 |
| 벡터의 연산 - 내적과 외적 (0) | 2022.06.09 |




