고정 헤더 영역
상세 컨텐츠
본문
📝 내적(Inner Product or Dot Product)
- 내적은 벡터 대수학에서 정의하는 두 가지 곱셈 중 하나이다.
- 두 벡터 사이의 연산이지만, 내적의 결과는 벡터가 아닌 스칼라 값이다.
- 벡터의 내적을 구하는 공식은 다음과 같다.
① u·v=uxvx+uyvy+uzvz
② u·v=||u||||v||cosθ
①는 두 벡터의 각은 모르고 벡터의 성분만을 알고 있을 경우 사용할 수 있는 공식이며,
②은 두 벡터의 각과 크기를 알고 있을 경우 사용할 수 있는 공식이다.
①의 식은 분명한 기하학적 의미를 보여주고 있지 않다. 코사인 법칙을 이용하면
u·v=||u||||v||의 관계를 발견할 수 있으며,
이는 두 벡터 간의 내적이 벡터 크기 배율을 가진 벡터 간 각도의 코사인임을 알 수 있다.
①을 2차원 벡터를 예를 들어 그림으로 표현하자면 다음과 같다.
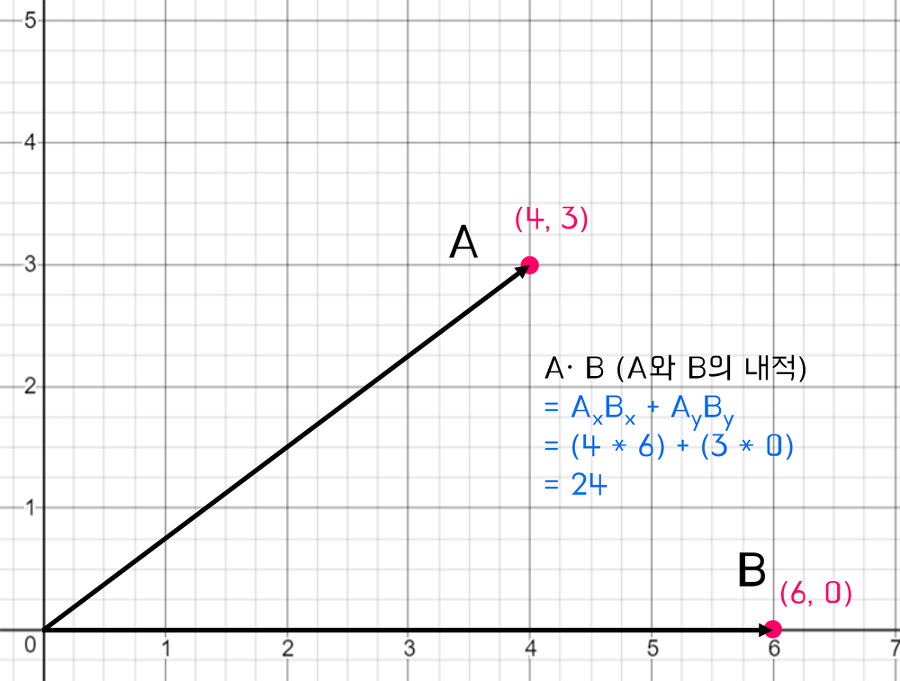
②를 2차원 벡터를 예를 들어 그림으로 표현하자면 다음과 같다.
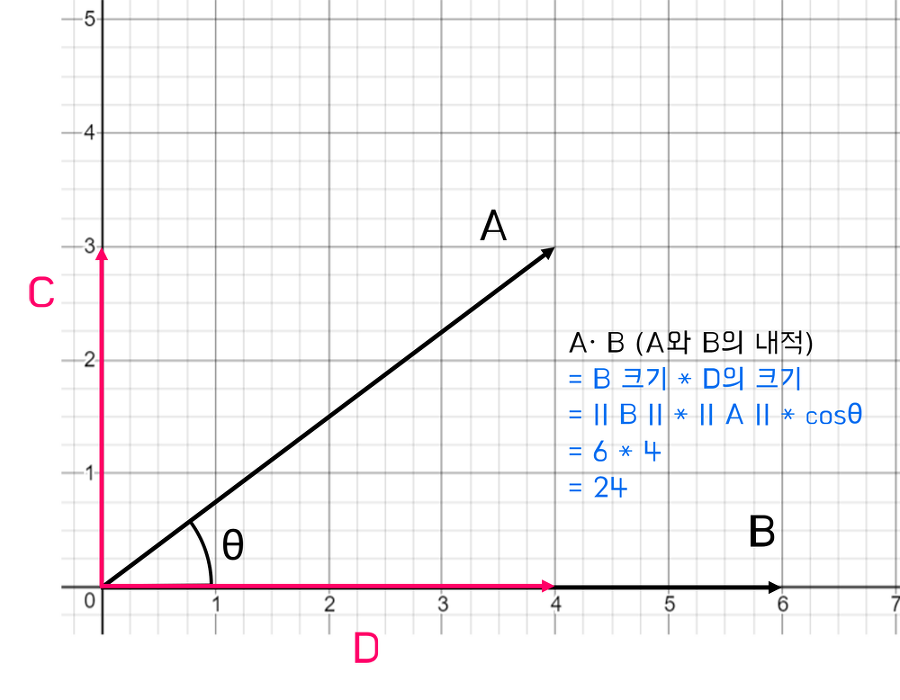
벡터 D의 크기는 A 벡터의 크기에 cosθ를 곱한 것이다.
||D||=||A||∗cosθ
여기서 A의 크기가 아닌, A를 분해한 벡터 D의 크기를 곱해주는 이유는
B 벡터에 실제로 영향을 주는 벡터가 D이기 때문이다.
한편 벡터 C는 벡터 B의 방향으로 어떤 영향도 주지 못하기 때문에, 내적 계산에서 무시한다.
▪️ 내적의 특성
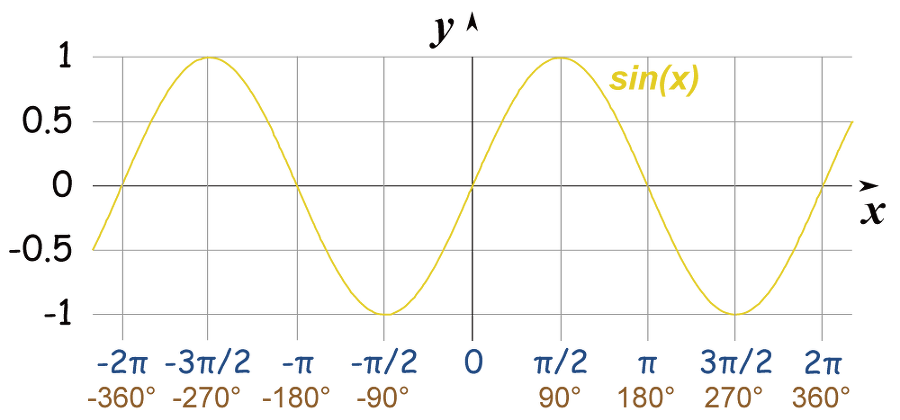
u와 v가 모두 단위 벡터인 경우 u·v는 두 벡터 간 각도의 코사인이 된다.
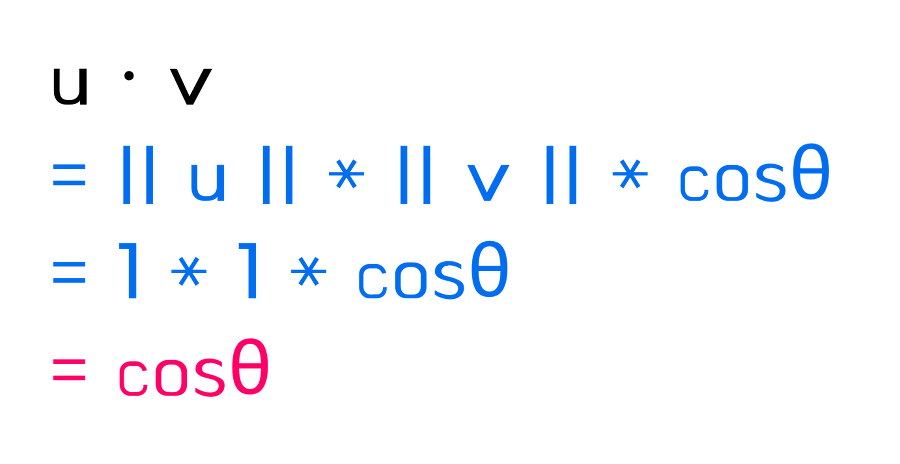
만약 u·v=0 이라면, 두 벡터는 직각이다.
만약 u·v>0 이라면, 두 벡터 간의 각도 θ는 90도(π2) 보다 작다.
만약 u·v<0 이라면, 두 벡터 간의 각도 θ는 90도(π2) 보다 크다.
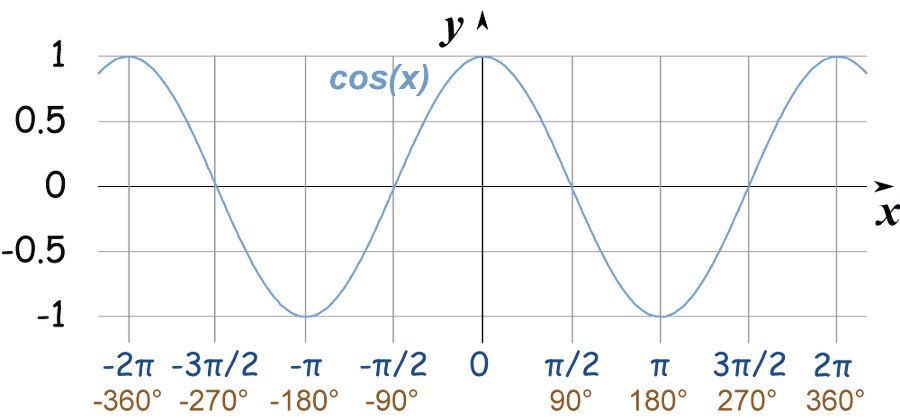
또한, 자기자신과 내적하면 자기자신 크기만큼의 제곱이다.
자기자신과 이루는 각도는 0도 이며, cos0=1이기 때문에 결과적으로 같은 벡터 2개를 내적하면 제곱이다.
▪️ 벡터의 내적 활용
첫째, 두 벡터의 사이각을 내적을 통해 구할 수 있다.
두 벡터의 성분을 알고 있다면, 크기를 알 수 있고 내적 계산을 이용해 arccosθ를 통해 구할 수 있다.
cosθ=a·b||a||||b||=axbx+ayby+azbz||a||||b||
θ=arccos(a·b||a||||b||)

둘째, 어떤 벡터 a에서 수직으로 내린 길이(투영 길이)를 구할 때 내적을 사용한다.
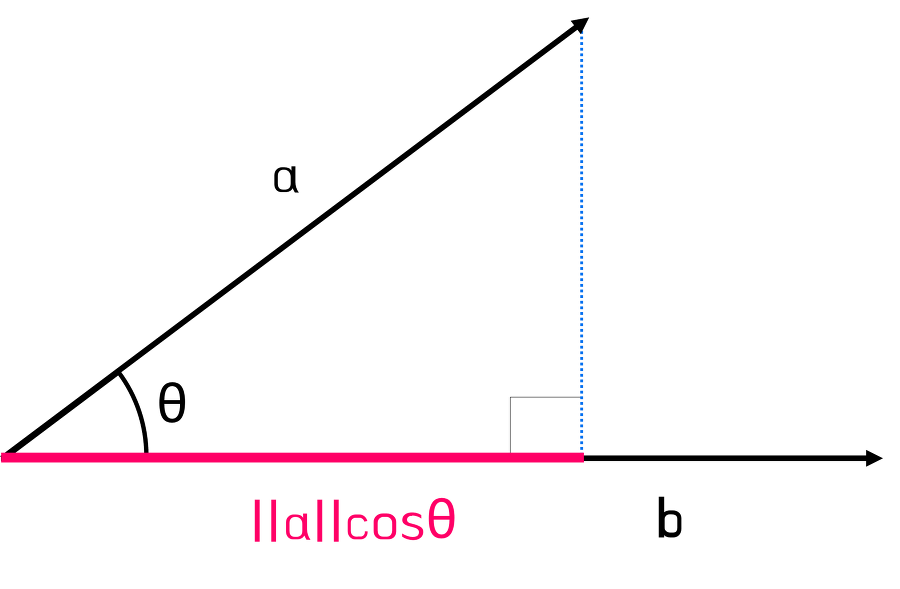
위의 그림에서 벡터 a의 투영길이를 구하고자 할 때는 벡터 b의 단위벡터를 이용한다.
벡터 b의 단위벡터의 길이는 1이며 내적 공식에 적용하면
a·b=||a||∗1∗cosθ가 되어
결국 투영길이는 ||a||cosθ가 된다.
또는 axbx+ayby+azbz에서 벡터 b의 단위벡터를 적용하면 된다.
투영 길이는 곧 벡터 b의 방향으로 얼마만큼 뻗어있는지 그 정도(크기)를 의미한다는 것을 알 수 있다.
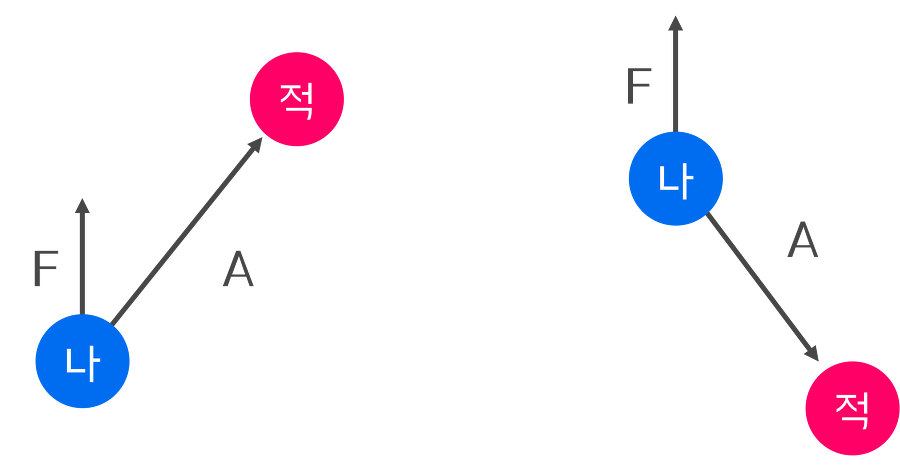
셋째, ‘나’의 방향벡터가 있을 때 적이 주인공의 앞에 있는지 뒤에 있는지 판단할 때 사용된다.
적의 위치에서 ‘나’의 위치를 뺀 벡터 즉, 내가 적을 바라보는 방향 벡터와 나의 Forward 벡터 간 내적을 했을 때,
각이 -90도 ~ 90도 사이에 있으면(cosθ가 양수이면) 적이 나의 앞에 있는 것이고,
각이 90도 ~ 270도 사이에 있으면(cosθ가 음수이면) 적이 나의 뒤에 있는 것이다.
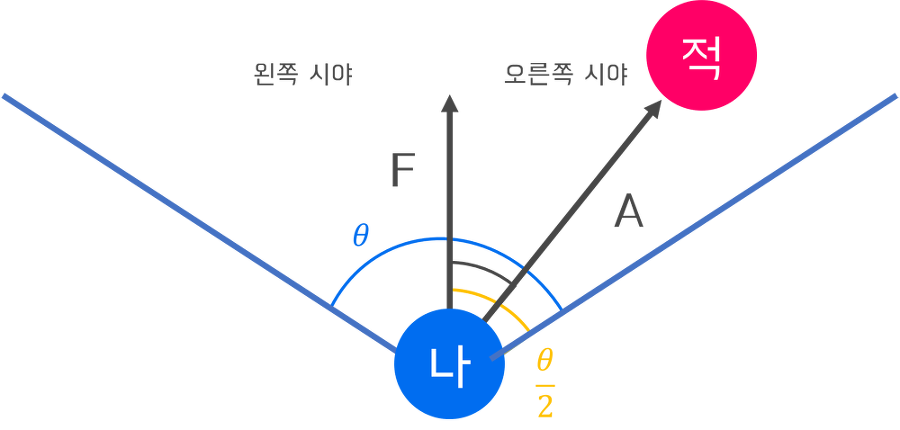
넷째, 적이 주인공의 시야각 안에 들어와 있는지 아닌지 판단할 때 사용된다.
‘나’의 시야각을 θ라고 하면,
Forward 벡터와 적과 '적의 위치에서 나의 위치를 뺀' 벡터 A 간의 내적을 통해 나오는 각도 값이
θ2를 넘지 않아야 시야각 내에 존재한다는 것을 판별할 수 있다.
다섯째, 점 A와 평면 S 간의 최단 거리를 구할 때 내적을 이용해 구할 수 있다.
(B는 평면 위의 점, d는 점 A와 평면 S 간의 최단 거리)
(A−B)·n=d
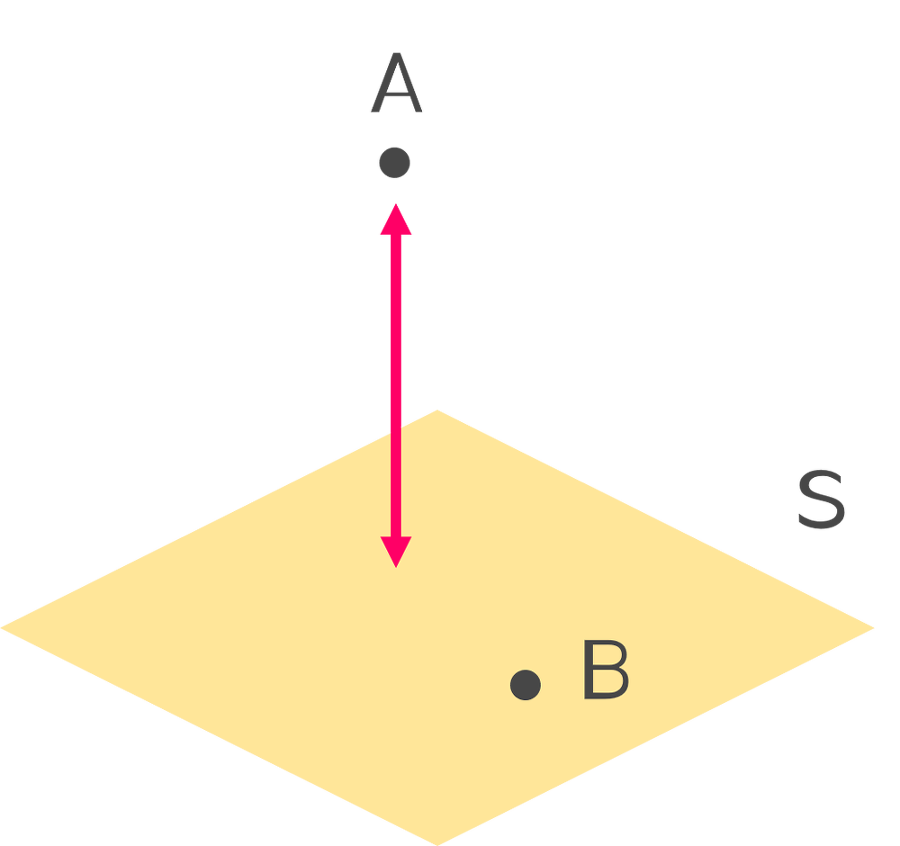
이는 단면을 그리면 좀 더 쉽게 이해된다.

벡터 BA와 평면의 법선 벡터(normal vector)와 내적을 구하면, ||BA||∗cosθ값이 된다.
이때, 평면의 법선 벡터는 정규화된 단위벡터라고 가정한다. ‘투영길이’를 떠올려보자. 이는 곧 점 A와 평면 S 간의 최단거리 d가 됨을 알 수 있다.
만약, 거리값이 0이면 A는 평면 위의 점이 된다.
여섯째, 선이 평면과 접하는 접점을 구할 때 내적이 사용된다.
(이 부분은 나중에 다시 정리)
📝 외적(Outer Product or Cross Product)
- 벡터 수학이 정의하는 두번째 형식의 곱은 외적이다.
- 스칼라로 계산되는 내적과는 달리, 외적의 결과는 또 다른 벡터이다.
- a와 b 두 벡터의 외적을 수행하면 다른 벡터 p를 얻으며, 이는 a와 b에 서로 직각을 이룬다.
즉, p는 a에 직각이며, p는 b에 직각이다.
- 벡터의 외적을 구하는 공식은 다음과 같다.
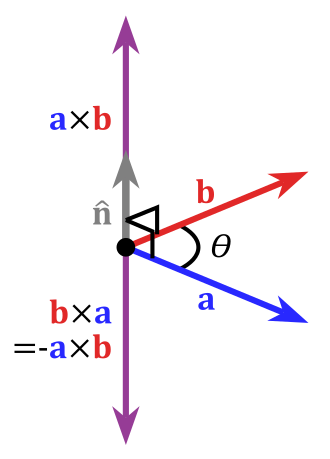
① p=a×b=n^||a||||b||sinθ
② p=a×b=[(aybz−azby),(azbx−axbz),(axby−aybx)]
①의 식을 자세히 살펴보면, n은 방향 벡터이고, 나머지는 값이기에 결과는 벡터라는 것을 알 수 있다.
또한, 외적 벡터의 크기는 두 벡터의 크기에 sinθ를 곱한 값과 같음을 알 수 있다.
②의 식은 다음과 같이 행렬식(Determinant)을 이용하여 간단히 쓸 수 있다.
(i=(1,0,0),j=(0,1,0),k=(0,0,1))
a×b 외적 벡터의 방향은 수학에서는 오른손 좌표계를 사용하며,
게임은 엔진이 사용하는 좌표계에 따라 다르다. (OpenGL에서는 오른손 좌표계, Unity나 Direct3D에서는 왼손 좌표계)
예를 들어, Direct3D는 왼손 좌표계를 사용하므로 왼손법칙에 따라 외적 벡터의 방향을 계산하지 않고도 알 수 있다.
왼손으로 첫번째 벡터 방향으로 손바닥을 맞춘 후, 두번째 벡터 방향으로 구부렸을 때
엄지손가락이 가리키는 방향이 바로 외적으로 리턴되는 벡터의 방향이 된다. (수학에서는 오른손 좌표계이니, 방향이 반대다. 헷갈리지 말 것!)
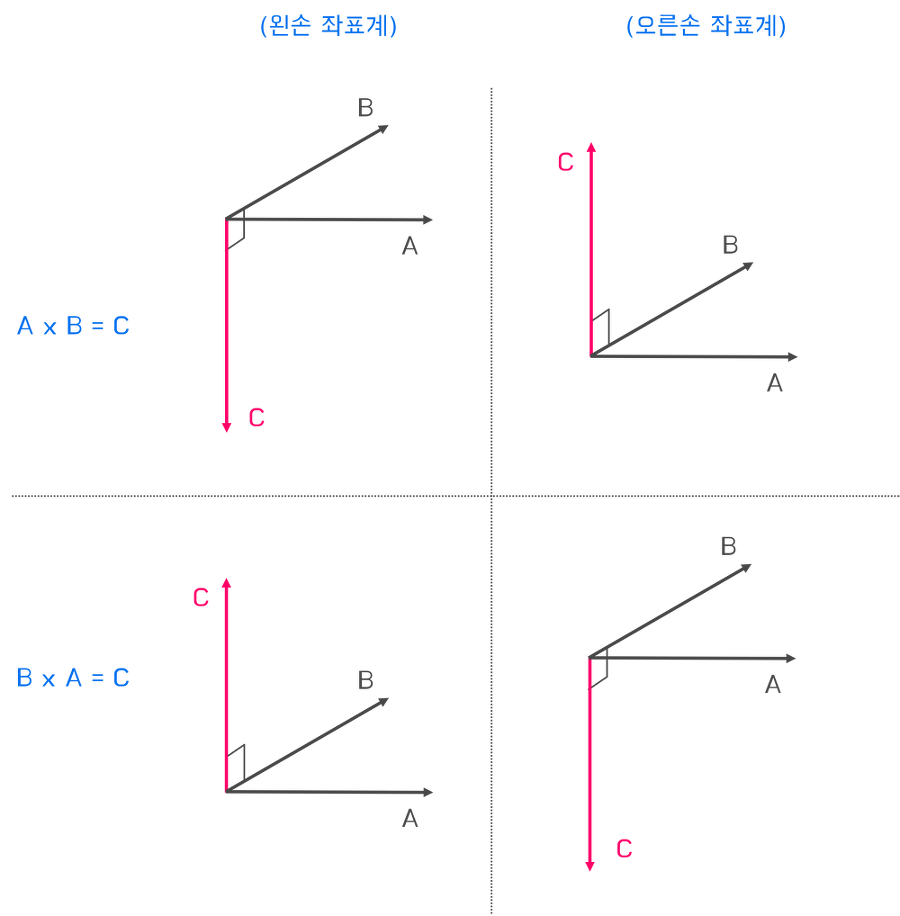
📌 연관 ▶ #왼손 좌표계와 오른손 좌표계
▪️ 외적의 특성
- 외적의 결과는 내적과 달리 벡터이기 때문에 방향과 크기를 동시에 가지게 된다.
방향: u×v⊥u 이고 u×v⊥v 이다.
즉, 두 벡터 u와 v 에 동시에 수직이다.
크기: 외적 벡터의 크기는 u 와 v를 변으로 하는 평행사변형의 넓이이다.
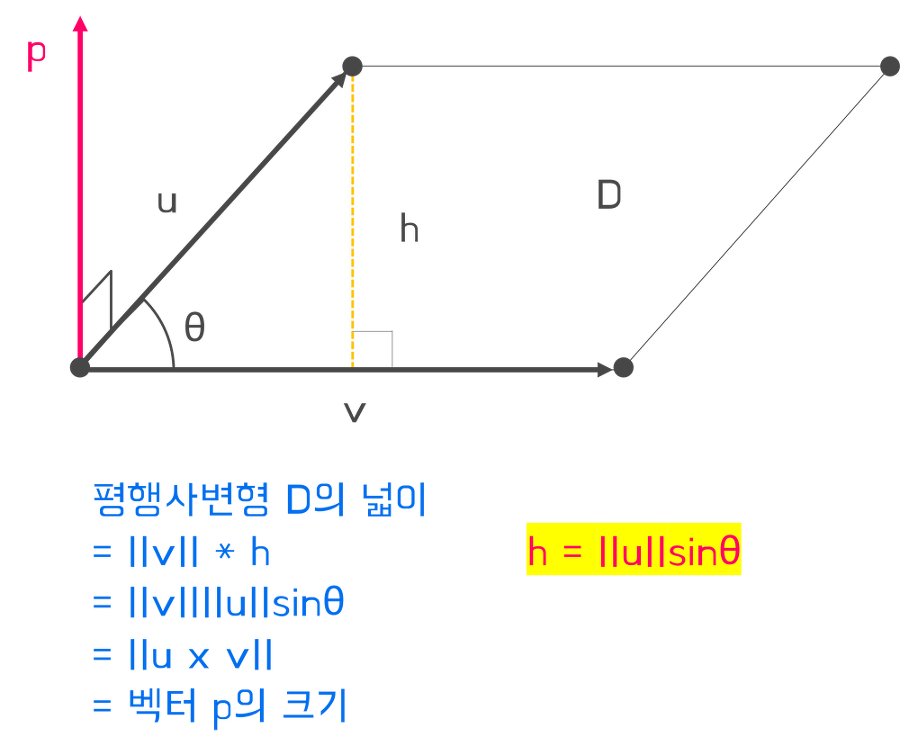
외적도 내적과 마찬가지로 주로 단위 벡터와 함께 사용되는데,
예를 들어 위의 그림에서 u와 v가 단위 벡터라면,
u와 v의 외적 결과값인 벡터 p의 크기로 u와 v의 사이각을 판단할 수 있다.
벡터 p의 크기가 1이라면 u와 v를 연결해서 만든 도형이 가로세로가 1인 정사각형임을 알 수 있고,
결국 벡터 u와 벡터 v가 수직임을 알 수 있다.
- 내적과 달리 교환 법칙이 성립하지 않으며, 순서를 바꾸면 반대 방향의 벡터가 나온다: u×v=−(u×v)
- 내적과 동일하게 분배 법칙은 성립한다: u×(v+w)=(u×v)+(u×w)
- 두 벡터가 모두 영벡터가 아닐때, u×v=0인 것은 u와 v가 서로 평행인 것과 동치이다.
즉, 두 벡터가 평행하면 크기는 0이다. (sinθ=0)
▪️ 벡터의 외적 활용
첫째, 평면의 법선 벡터를 구할 때 사용한다.
삼각형의 세 점을 알고 있다고 할 때, 벡터 2개를 구할 수 있게 되고
그 두 벡터를 외적하면 해당 삼각형이 속한 평면의 법선 벡터를 구할 수 있다.
입체적으로 보자면 이런 느낌...

또한, 삼각형의 넓이를 구할 때도 외적을 사용할 수 있다.
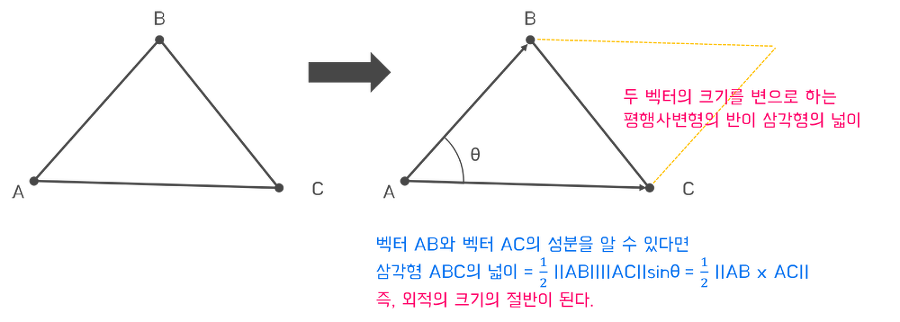
둘째, 평면이 앞면인지 뒷면인지를 알아낼 수 있고, 따라서 컬링(culling)할 때 사용된다.
법선 벡터가 한 평면의 뒤를 가리킨다면, 뒷면을 화면 출력에서 제외되는 면이 된다.
이와 같이 보이지 않는 뒷면을 화면 출력에서 제외시키는 것을 백페이스 컬링(backface culling)이라고 하며,
Direct3D에서는 컬링 옵션에 따라 출력에서 제외시키거나 출력하게 할 수 있다.
컬링의 기준이 되는 것이 바로 이 법선 벡터의 방향이다.
eye 벡터와 평면의 법선 벡터의 내적으로부터 얻는 cosθ 값을 사용하면 앞과 뒤를 판단할 수 있다.
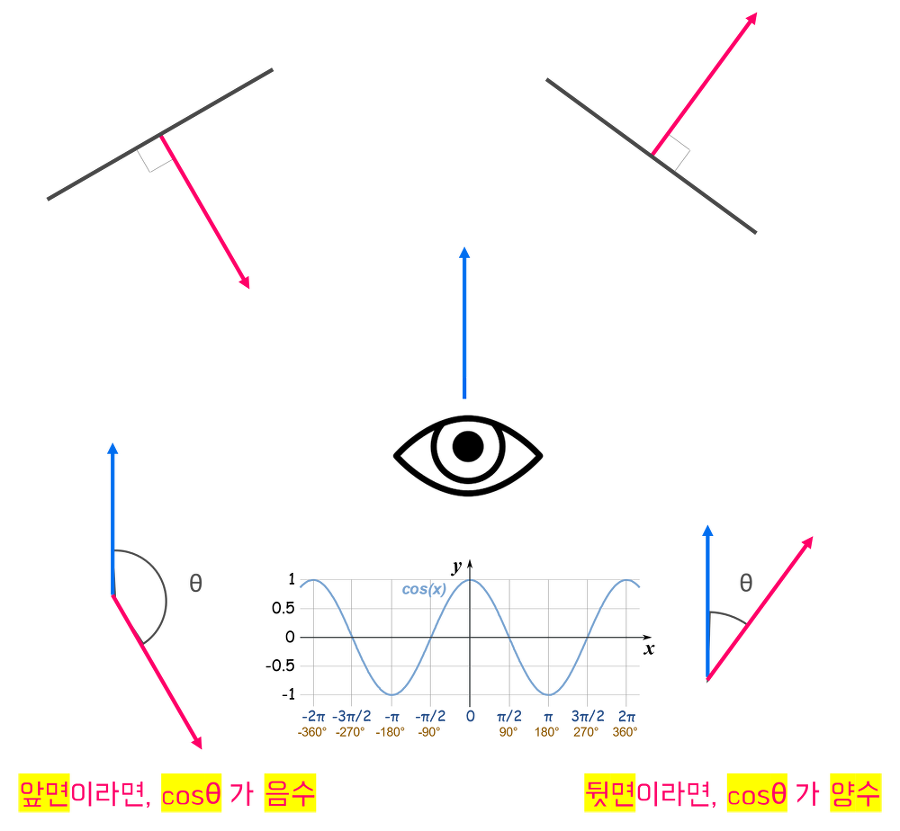
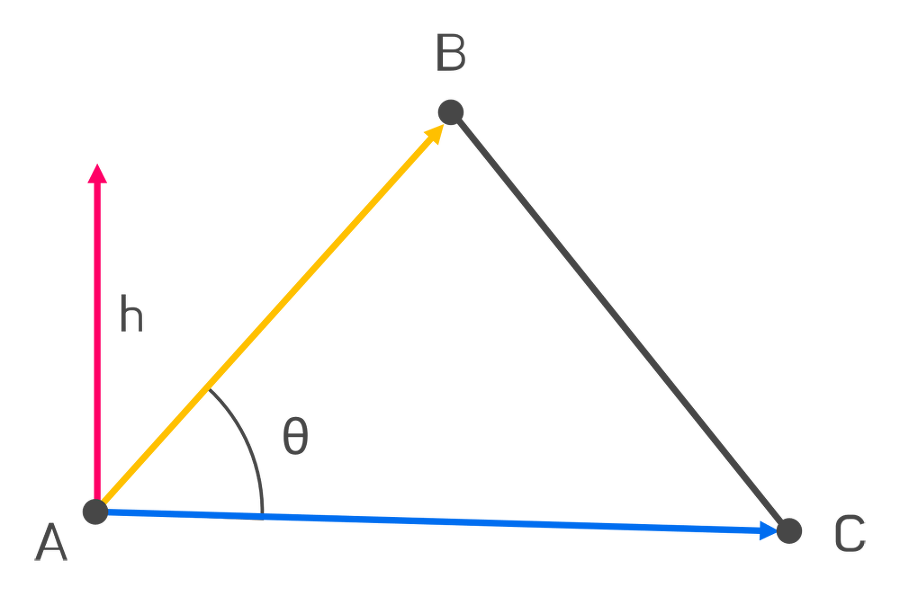
셋째, 점과 직선사이의 거리를 구할 때 사용된다.
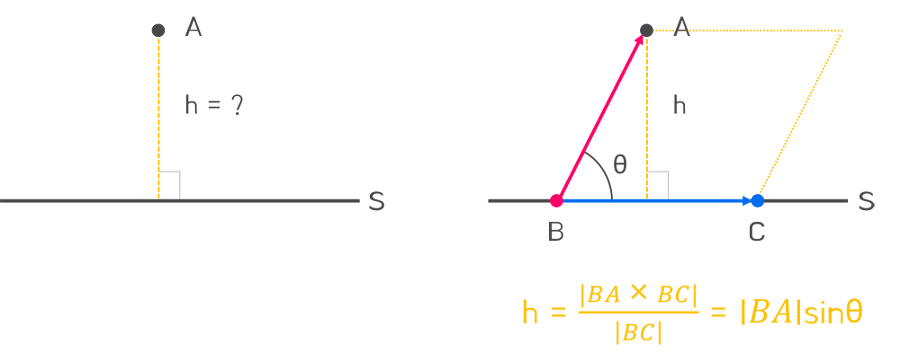
직선 S의 위의 점 B와 C를 임의로 선택한다.
BA 와 BC 벡터를 만들어, 평행사변형의 높이를 구하는 방법을 응용해
문제를 풀 수 있다.
넷째, 빛의 방향과 평면의 법선 사이의 각도를 이용해 평면에 적용될 빛의 영향을 결정하게 된다.
만약 빛을 평면에 비추고 싶다면, 평면을 이루는 각 벡터 정보에는 법선 벡터에 대한 정보가 반드시 있어야한다.
'Study > Discrete math' 카테고리의 다른 글
| 벡터 대수 (0) | 2023.02.05 |
|---|---|
| 벡터의 외적(Cross Product)과 내적(Inner Product) (0) | 2022.10.25 |
| 왼손 좌표계(Left-handed coordinate system)와 오른손 좌표계(Right-handed coordinate system) (0) | 2022.06.09 |
| 벡터의 연산 - 덧셈과 뺄셈, 분해 (0) | 2022.06.09 |
| 벡터(vector)와 스칼라(scalar) (0) | 2022.06.09 |




